カシミール力
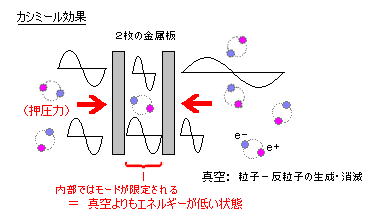
真空中に平行に置かれた2枚の導体板の間には引力が働く。この現象はカシミール効果と呼ばれ、通常は次のように説明されている。
導体の間の空間に生じる電磁場の量子揺らぎの零点エネルギーは導体間の距離の関数になり、導体が近づくほど、間の空間にあるエネルギーは低くなる。すなわち、導体間に引力が働 いていることになる。
2枚の平行金属板の間の電磁場は、金属板の間に整数個の波が立ったモードの重ね合わせでかけるが、量子化するとそれぞれのモードの零点振動が零点エネルギーを持つ。極板間の真空は周囲の真空よりエネルギーが下がった状態に置かれ引力を生じる。
この引力は、カシミールらによって予言され(1948、オランダ、フィリップス研)、近年 ラモロー(Steve K. Lamoreaux)によって実験的に確認され(1997、米国・ロスアラモス国立研・・・原爆の開発で有名)、また多くの研究機関でその事実が確認されている。
場の量子論では、”電磁場の量子”である光子は、調和振動子で記述され、 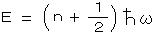 のエネルギーを持っている。
のエネルギーを持っている。
この調和振動子は、n = 0 の 最低エネルギー状態(= 電磁場の真空)ではそれぞれの周波数に対応した零点振動が存在し、
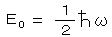 ・・・・・ ①
・・・・・ ①
のエネルギーを伴っている。
このように、真空は仮想的な光子の生成・消滅で満ちていることになる。(光子だけではなく、電子・陽電子などのあらゆる粒子・反粒子の生成・消滅の場としてもよい。)
ここで、2枚の”完全導体板”という理想的な状態において、近接した2枚の平行導体板が存在するとき、その内部と外部にはエネルギー密度の差が存在することになり、これらの零点振動を周波数(モード)について総和すると、エネルギー密度は、
 ・・・・・・ ②
・・・・・・ ②
カシミールエネルギーの計算では、この(無限大)-(無限大)から有限値を得るために、ゼータ関数 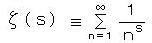 による繰り込みが必要である。
による繰り込みが必要である。
ゼータ関数はオイラー積 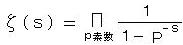 で表わされ、
で表わされ、
領域 d 間のカシミールエネルギー密度は、 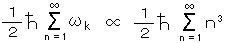 で書けるので、 s = -3、すなわち ζ(-3) を求めることに帰着される。
で書けるので、 s = -3、すなわち ζ(-3) を求めることに帰着される。
ζ(-n) = -Bn+1/(n + 1) Bn: ベルヌーイ数 より、 ζ(-3) = -(-1/30)/4 = 1/120
※ 注) この繰り込み理論に重大な誤りがある(↓)
この ⊿V を z方向の距離 d で偏微分すると、単位面積あたりの力(引力)となり、これが代表的なカシミール力である。
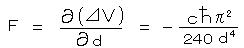 、 F ≒ -1.30×10-7/d(μm)4 (N/cm2)
、 F ≒ -1.30×10-7/d(μm)4 (N/cm2)
また、一方が平面、もう一方が球(半径 R)の場合(1948年にカシミールが予測した境界条件)は、
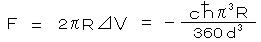 、 F ≒ -2.72×10-9×R(m)/d(μm)3 (N)
、 F ≒ -2.72×10-9×R(m)/d(μm)3 (N)
* カシミール力は、境界条件に強く依存し、引力にも斥力にもなり得る。また、実際のカシミール力は、導電率、面粗さ、温度などの要因によりそれぞれの場合が理論計算されている。
( → 流体(エタノール)中の金属についての斥力の場合の実証報告)
カシミール効果の単位面積当りの力は非常に小さく、たとえば、一辺が200キロメートルの正方形の金属板が1μmの間隔で置かれた場合、そのエネルギーは100ワットの電球を1秒間光
らせる程度である。 しかし、近年は、遠隔的に斥力を発生させることを追求している所もあり、メタマテリアル、アシンメトリックマテリアル(一方通行素材)(下*)に関わって世界中で研究され始めている。 (→ セント・アンドリュース大学)
* 場の理論によるカシミール力は、揺らぎによる場の零点エネルギーをすべてのモードについて足し合わせたものは発散してしまう。この、”無限大”から”無限大”を引いて”有限量”を求めるという”繰り込み操作”をしないで、揺らぎによって生じる電磁場が導体表面に誘起する電荷と電流に、揺らぎによる電磁場自身がおよぼすローレンツ力を計算し、(ゼロ点エネルギーという概念を通さず)直接にカシミール力を求める試みもなされている。
* (参考HP) → カシミール効果のねじれ秤による精密測定(by.東大宇宙線研、2005)、 場の量子論におけるカシミール効果
※ 注) (2015 11)
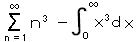 は、
は、 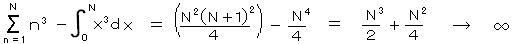 (N → ∞)
(N → ∞)
となって 発散は消えない。(理論は間違い!)
そこで、 x = 0 の近傍で f(x) = 1、 x = ∞ で x3・f(x) = 0 となるような f(x) を想定(たとえば 1/(1 + x4) のような)し、それぞれにかけて、
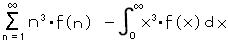 のように変形する。 g(x) = x3・f(x) とおき、 オイラー・マクローリンの和公式より、
のように変形する。 g(x) = x3・f(x) とおき、 オイラー・マクローリンの和公式より、
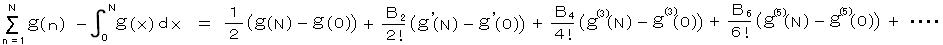
f(x) の定義より、 N → ∞ のとき g(N) → 0、 g’(N) →
0、 g(3)(N) → 0、 g(5)(N) → 0、 ・・・・
また、 g(0) = 0、 g’(0) = 0、 g(3)(0) = 6、 g(5)(0) = 0、 ・・・・
ベルヌーイ数 Bn は、 B0 = 1、 B1 = -1/2、 B2 = 1/6、 B3 = 0、 B4 = -1/30、 B5 = 0、 B6 = 1/42、 ・・・・
したがって、
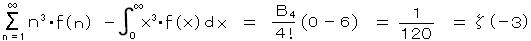
のように、 上記の関数 f(x) を想定するならば、数論的定数 1/120 が導かれる。
∴ 理論が間違っているにもかかわらず、ラモローによって実際にカシミール力が観測されるということは、宇宙空間に さらに複雑な”数論的な”メカニズムが存在することを意味している。
→ 参考リンク
§ 創世記1章のあかし:
上記の式①は、エネルギー E と 時間 t (ω=2πf =2π/T(T:周期))の関係式です。エネルギーはニュートン力学では距離のデメンションを含んで定義されますが、このエネルギーを距離を用いずにそのまま基本的なパラメータとして定義します。すると、量子力学的な(確率性による)水面下の波動は、プランク定数を比例定数として単純に①のように設定されます。プランク定数は、量子変換の”窓”です。
「そのとき、神が、「光よ、あれ。」と仰せられた。すると光ができた。(第1日)」(創世記1:3)
次に、②式のように、3次元の空間の広がりが設定されました。2枚の金属板という境界条件が、z方向の波動に特別な意味をもたらしたのです。間隔
d のモードの総和と 全モードの総和はどちらも無限大ですが、その差は、実にエレガントな有限値に落ち着きます。このエレガントさは、数論と複素関数論の本質的なところにかかわっています。(→(参考)) 空間距離という被造物が創造されて初めて、その具体的な形が決まりました。
「ついで神は、大空を造り、大空の下にある水と、大空の上にある水とを区別された。(第2日)」(創世記1:7)
このように、第1日の「光」が第1であり、次に、第2日の「大空」の創造が続き、「光(時間とエネルギーで構成される量子)」は「大空(一般的な3次元空間・距離の概念)」よりも根源的な存在ということになります。
(第3日(木や植物)、第4日(星、宇宙の天体)、第5日(動物)、第6日(人間)は、DNAという 人間が人工的に作ることができない複雑の極致の構造物、あるいは、地球外の単純でかさばった大量の物質が、これら第1日、第2日の土台の上に造られていきました。 * 「大空(空間)」の創造の第2日については、他の創造に対して言われている「良し」という神様の祝福の言葉が無いのは、エントロピーの増大による宇宙の老化(exp(-αt)の”死の形象”)がすでにこのときから始まったため。)
* 天地万物(被造物)は、(御使い、悪霊も含めて)すべて「時間」の流れの中に置かれています。ただ、神様(創造主)だけが、この「時間」を超越した存在です。
預言の賜物は、唯一、未来を持ってくる賜物であり、神様の「三位一体」の中心ポイントにあります。御子イエス様は、「神の子」であると同時に、時間を超越した「神」です。
また、旧約聖書のヘブライ語の文法は、完了体と未完了体で書かれています。神様の前には、すべてのことはすでに「完了」しているのです。この「完了体」は「信仰による創造・再創造」の表現に適用されます。神様は、「ことばの神」です。
「イエスのあかしは預言の霊です」(黙示録19:10) ・・・ イエス様の時間を超越した”神性”を表わすみことば
トップへ戻る

 ・・・・・・ ②
・・・・・・ ②